Here at Zinkerz, we closely monitor trends in the SAT to bring our students the most up-to-date test-taking strategies. We try to get inside the minds of the test makers to help our students out-think the exam! Let’s review some algebra topics popping up on the SAT recently and tackle the best way to solve them!
Using the Discriminant
These questions will ask you to make a statement about the value of some unknown constant or coefficient in a given equation. To help you do this, the question will provide information about the number of solutions for that equation. This is a clue that will lead us to the best strategy for solving!
If a question tells you about the number of solutions for a given quadratic equation, you should immediately think of the discriminant. Recall:
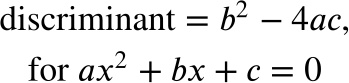
The discriminant should look familiar! Recall the quadratic formula:
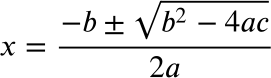
The discriminant comes directly from beneath the square root and tells us the following:

If you can remember these three conditions when calculating the discriminant, these problems will be easy to solve. Let’s do an example!
Problem 1:
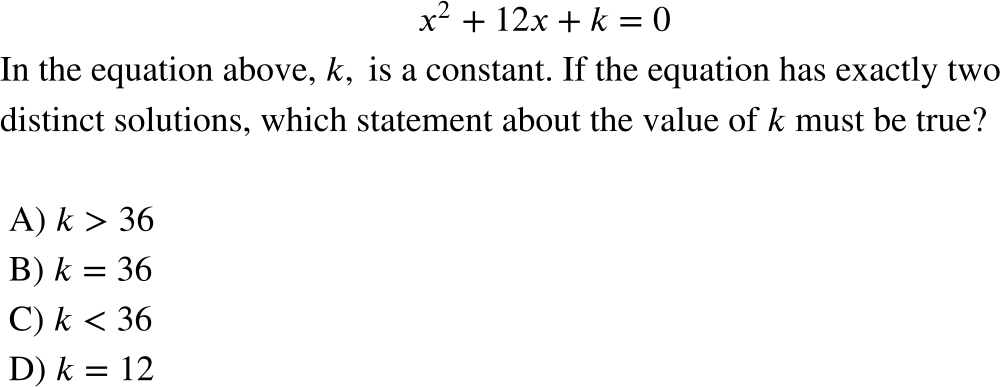
Step 1: Identify a, b, and c from the given equation.
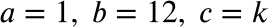
Step 2: Because our equation has two distinct solutions, we will use the third condition of the discriminant to solve for k:
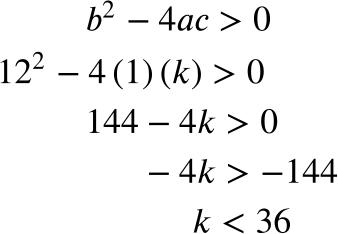
Completing the Square
These questions will give you an equation for a circle and ask you to find the radius. This seems simple enough, except that the given equation is not in the form that is most conducive to recognizing the radius. These types of questions aim to get the given equation in standard circle form by completing the square. Recall the standard form for the equation of a circle:
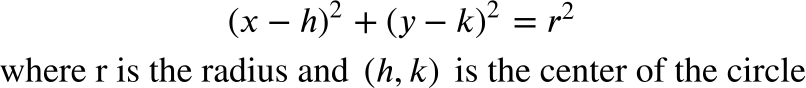
Once in this form, the circle’s radius is easily identifiable on the right side of the equation. Let’s look at an example, remembering that we will need to complete the square two times to achieve our goal.
Problem 2:
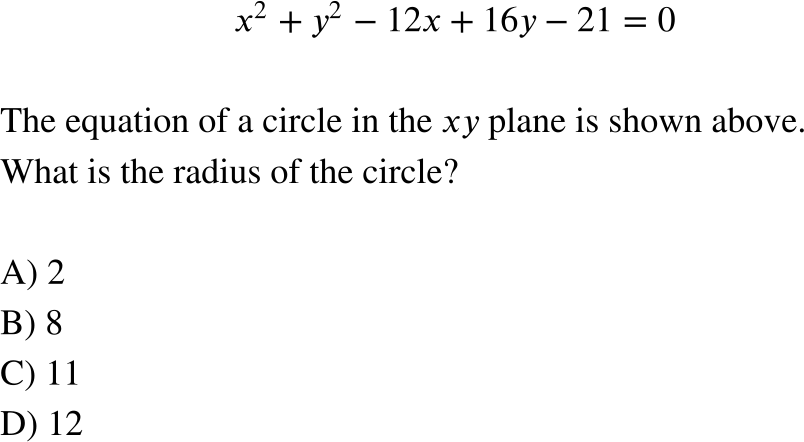
Let’s solve the following:

Picking the Correct Form
These questions will ask you to choose an equivalent form of the given equation where certain numbers appear in specific spots. The question will have hints about how to manipulate or solve the given equation to get it correct. Let’s look at an example:
Problem 3:

The answer choices here may look a bit overwhelming, but a hint points us to the right one. The question asks us to look for the vertex coordinates in the equivalent form. We can use this vertex “clue” in a couple of ways:
Find the vertex (or part of it):
Remember that the equation for finding the x coordinate of the vertex point of a quadratic equation is:
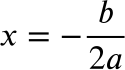
Once you have the x coordinate, look for an answer choice where that number appears. Without also finding the y coordinate by plugging the x coordinate back into the original equation, we may only be able to narrow down our answer choices. By finding the x coordinate of the vertex, we will have one of the pieces we need to pick the right form.
Look for vertex form:
The question asks us to find the equivalent form with both coordinates of the vertex. Luckily, we know of a form that displays this: vertex form! Recall:
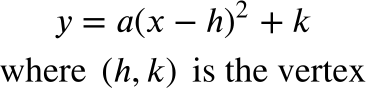
Look for an answer choice that is written in vertex form. This choice will have the coordinates of the vertex. You will know the value of a since it comes from the original equation, and h will be the x coordinate we found with the above formula.
You may only need to use one of these hints to be able to choose the right answer, so be sure to use your time efficiently. Between all these pieces of information, you can select the correct form!
Percent Change
These questions will ask you to write an expression representing a certain variable after some kind of percent change (increase or decrease). The trick to these questions is thinking of percents as whole numbers or decimals and understanding the algebraic relationship in the change of value. Let’s look at an example:
Problem 4:

To calculate the “resulting value” of b, think about it as the sum of the “initial value” (or the original value, b) and the “additional value” (or the percent increase or decrease that has occurred). The initial value will be 100% of the value of b, or 1b, and the additional value will be 600% of the value of b, or 6b. Take a look at the equation below:
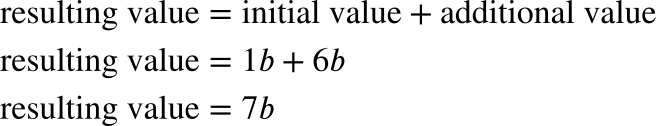
Don’t make these types of problems harder than they need to be! Oftentimes, the resulting equation is effortless to solve.
Rational Exponents and Radicals
These questions will ask you to choose the equivalent form of the given expression that contains rational exponents. This may require you to convert radicals to rational exponents or perform operations involving rational exponents to simplify. Sounds complicated? Remember these rules (tricks) to help you:
![2 lines Line 1: x to the a.-th power times x to the power of b equals x raised to the a. plus b power the fraction with numerator x to the a.-th power and denominator x to the power of b equals x raised to the a. minus b power Line 2: x to the a.-th power to the power of b equals x raised to the a. times b power x raised to the a. over b power equals the b-th root of x to the a.-th power <math xmlns="http://www.w3.org/1998/Math/MathML" display="block" data-is-equatio="1" data-latex="begin{array}{l}x^acdot x^b=x^{a+b}& frac{x^a}{x^b}=x^{a-b}\
left(x^aright)^b=x^{acdot b}& x^{frac{a}{b}}=sqrt[b]{x^a}end{array}"><mtable columnalign="left" columnspacing="1em" rowspacing="4pt"><mtr><mtd><msup><mi>x</mi><mi>a</mi></msup><mo>⋅</mo><msup><mi>x</mi><mi>b</mi></msup><mo>=</mo><msup><mi>x</mi><mrow data-mjx-texclass="ORD"><mi>a</mi><mo>+</mo><mi>b</mi></mrow></msup></mtd><mtd><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mfrac><msup><mi>x</mi><mi>a</mi></msup><msup><mi>x</mi><mi>b</mi></msup></mfrac><mo>=</mo><msup><mi>x</mi><mrow data-mjx-texclass="ORD"><mi>a</mi><mo>−</mo><mi>b</mi></mrow></msup></mtd></mtr><mtr><mtd><msup><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">(</mo><msup><mi>x</mi><mi>a</mi></msup><mo data-mjx-texclass="CLOSE">)</mo></mrow><mi>b</mi></msup><mo>=</mo><msup><mi>x</mi><mrow data-mjx-texclass="ORD"><mi>a</mi><mo>⋅</mo><mi>b</mi></mrow></msup></mtd><mtd><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><msup><mi>x</mi><mrow data-mjx-texclass="ORD"><mfrac><mi>a</mi><mi>b</mi></mfrac></mrow></msup><mo>=</mo><mroot><msup><mi>x</mi><mi>a</mi></msup><mi>b</mi></mroot></mtd></mtr></mtable></math>](https://zinkerz.com/wp-content/uploads/2023/09/image-14.png)
These rules work when we simplify and perform operations on numbers with the same base. Furthermore, remember to follow the order of operations, so you don’t confuse yourself. Do one step at a time and keep your written work organized. Let’s try an example:
Problem 5:
![5 lines Line 1: Which expression is equivalent to b raised to the 11 over 12 power times b raised to the five fourths power raised to the exponent two thirds end exponent comma where b is greater than 0 question mark Line 2: cap A close paren the sixth root of b to the 11th power Line 3: cap B close paren the fourth root of b to the fifth power Line 4: cap C close paren the sixth root of b to the fifth power Line 5: cap D close paren the cube root of b to the fourth power <math xmlns="http://www.w3.org/1998/Math/MathML" display="block" data-is-equatio="1" data-latex="begin{array}{l}text{Which expression is equivalent to }b^{frac{11}{12}}left(b^{frac{5}{4}}right)^{frac{2}{3}},text{ where }b>0?\
text{A)} sqrt[6]{b^{11}}\
text{B)} sqrt[4]{b^5}\
text{C)} sqrt[6]{b^5}\
text{D)} sqrt[3]{b^4}end{array}"><mtable columnalign="left" columnspacing="1em" rowspacing="4pt"><mtr><mtd><mtext>Which expression is equivalent to </mtext><msup><mi>b</mi><mrow data-mjx-texclass="ORD"><mfrac><mn>11</mn><mn>12</mn></mfrac></mrow></msup><msup><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">(</mo><msup><mi>b</mi><mrow data-mjx-texclass="ORD"><mfrac><mn>5</mn><mn>4</mn></mfrac></mrow></msup><mo data-mjx-texclass="CLOSE">)</mo></mrow><mrow data-mjx-texclass="ORD"><mfrac><mn>2</mn><mn>3</mn></mfrac></mrow></msup><mo>,</mo><mtext> where </mtext><mi>b</mi><mo>></mo><mn>0</mn><mo>?</mo></mtd></mtr><mtr><mtd><mtext>A)</mtext><mtext></mtext><mroot><msup><mi>b</mi><mrow data-mjx-texclass="ORD"><mn>11</mn></mrow></msup><mn>6</mn></mroot></mtd></mtr><mtr><mtd><mtext>B)</mtext><mtext></mtext><mroot><msup><mi>b</mi><mn>5</mn></msup><mn>4</mn></mroot></mtd></mtr><mtr><mtd><mtext>C)</mtext><mtext></mtext><mroot><msup><mi>b</mi><mn>5</mn></msup><mn>6</mn></mroot></mtd></mtr><mtr><mtd><mtext>D)</mtext><mtext></mtext><mroot><msup><mi>b</mi><mn>4</mn></msup><mn>3</mn></mroot></mtd></mtr></mtable></math>](https://zinkerz.com/wp-content/uploads/2023/09/image-15.png)
Notice how all answer choices are written as one term involving a radical? This is a cue for simplifying our given expression and converting our rational exponents. Since each term has the same base (b), we can follow the rules above to get the correct answer quickly.
![5 lines Line 1: b raised to the 11 over 12 power times b raised to the five fourths power raised to the exponent two thirds end exponent equals b raised to the 11 over 12 power times b raised to the 10 over 12 power Line 2: equals b raised to the 11 over 12 plus 10 over 12 power Line 3: equals b raised to the 22 over 12 power Line 4: equals b raised to the eleven sixths power Line 5: equals the sixth root of b to the 11th power <math xmlns="http://www.w3.org/1998/Math/MathML" display="block" data-is-equatio="1" data-latex="begin{array}{l}b^{frac{11}{12}}left(b^{frac{5}{4}}right)^{frac{2}{3}}=&b^{frac{11}{12}}cdot b^{frac{10}{12}}\
=&b^{frac{11}{12}+frac{10}{12}}\
=&b^{frac{22}{12}}\
=&b^{frac{11}{6}}\
=&sqrt[6]{b^{11}}end{array}"><mtable columnalign="left" columnspacing="1em" rowspacing="4pt"><mtr><mtd><msup><mi>b</mi><mrow data-mjx-texclass="ORD"><mfrac><mn>11</mn><mn>12</mn></mfrac></mrow></msup><msup><mrow data-mjx-texclass="INNER"><mo data-mjx-texclass="OPEN">(</mo><msup><mi>b</mi><mrow data-mjx-texclass="ORD"><mfrac><mn>5</mn><mn>4</mn></mfrac></mrow></msup><mo data-mjx-texclass="CLOSE">)</mo></mrow><mrow data-mjx-texclass="ORD"><mfrac><mn>2</mn><mn>3</mn></mfrac></mrow></msup><mo>=</mo></mtd><mtd><msup><mi>b</mi><mrow data-mjx-texclass="ORD"><mfrac><mn>11</mn><mn>12</mn></mfrac></mrow></msup><mo>⋅</mo><msup><mi>b</mi><mrow data-mjx-texclass="ORD"><mfrac><mn>10</mn><mn>12</mn></mfrac></mrow></msup></mtd></mtr><mtr><mtd><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mo>=</mo></mtd><mtd><msup><mi>b</mi><mrow data-mjx-texclass="ORD"><mfrac><mn>11</mn><mn>12</mn></mfrac><mo>+</mo><mfrac><mn>10</mn><mn>12</mn></mfrac></mrow></msup></mtd></mtr><mtr><mtd><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mo>=</mo></mtd><mtd><msup><mi>b</mi><mrow data-mjx-texclass="ORD"><mfrac><mn>22</mn><mn>12</mn></mfrac></mrow></msup></mtd></mtr><mtr><mtd><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mo>=</mo></mtd><mtd><msup><mi>b</mi><mrow data-mjx-texclass="ORD"><mfrac><mn>11</mn><mn>6</mn></mfrac></mrow></msup></mtd></mtr><mtr><mtd><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mtext></mtext><mo>=</mo></mtd><mtd><mroot><msup><mi>b</mi><mrow data-mjx-texclass="ORD"><mn>11</mn></mrow></msup><mn>6</mn></mroot></mtd></mtr></mtable></math>](https://zinkerz.com/wp-content/uploads/2023/09/image-16.png)
The Math section of the SAT doesn’t have to be scary! Practice the problems that give you the most trouble and master the foundational topics in algebra and geometry. Remember to use these tips and tricks to use the limited time efficiently.
You got this!



